TIMBER AND BEAM DEFLECTION, according to Eurocode 5

How the software check for serviceability of the structure according to the technical standards in APF WoodBeam and APF WoodTruss.

Serviceability means the structure must appear safe and comfortable to the people who use it, excessive floor deflection could worry the people in a building. APF WoodTruss and APF WoodBeam perform serviceability checks in accordance with Eurocodice 5 (EN 1995-1-1:2004 + A1:2008 + A2:2014).

The timber deformation factor

In Eurocode 5 the deflection of a member is required at two stages:

Immediately when action are applied.

After time-dependent deformation has taken place.

Instantaneous and creep deformations are related by the deformation factor k_def :

ucreep = kdef uinst

The final deflection u_fin may be obtained by superimposing the creep deformations u_creep on the instantaneous deformation u_inst

The deformation factor k_def also appears in the relationships between the mean and final mean value of the modulus of elasticity (and shear modulus, and slip modulus) for example:

Emean,fin = Emean / (1 + kdef)

The ULS, first-order, linear elastic analyses

If the distribution of member forces and moments is affected by the stiffness distribution in the structure, for example when the structure is composed by different materials or materials with different time-dependent properties, the internal actions have to be derived using the final mean value dof the modulus of elasticity, for example:

Emean,fin = Emean / (1 + ψ2 kdef)

On the other hand, if this does not happen, when the stiffness distribution within the structure does not affect the distribution of internal stress resultants, for example where all material being used have the same time-dependent properties, the internal actions have to be derived using the mean value of the modulus of elasticity E_mean

For second-order linear elastic analyses, design values of the modulus of elasticity (not adjusted for duration of load) must be used, for example:

Ed = Emean / γM

Below are some excerpts from the published technical standard:

The SLS analyses for timber structures

At the instantaneousconditions, Eurocode 5 uses the characteristic load combination to derive the deformation of members. In this short-term situation, the creep behaviour of the member is not relevant (it has not yet had any effect on the structure), deformations have to be derived using the mean value of the modulus of elasticity E_mean

At the final conditions, Eurocode 5 uses the quasi-permanent load combination to derive the deformation of members. The final deflection u_fin should be obtained by superimposing the creep deformations u_creep on the instantaneous deformation u_inst

For structures consisting of members, components and connections with the same creep behaviour, the total deflection will be the superimposition of the creep deformation calculated with the quasi-permanent combination on the instanteneouns deformation calculated for the characteristic combination of actions, where the final deformation can then be written as:

ufin = ucreep + uinst = uinst (1 + kdef)

If he structure consists of members having different creep behaviour, the creep deformation should be calculated using the quasi-permanent combination of actions with the final mean value of the modulus of elasticity, and the final deflection is obtained adding the instantaneous deformation due to the difference between the characteristic and the quasi-permanent combination of actions (calculated using the mean value of the modulus of elasticity).

Below are some excerpts from the published technical standard:

 WoodBeam & WoodTruss

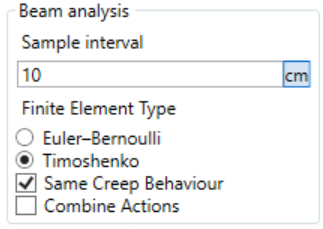
In APF WoodBeam and APF WoodTruss, the settings dialog window contains the following options : Combine Actions and Same Creep Behaviour

In APF WoodBeam and in APF WoodTruss, the internal actions and deformations are evaluated with two models:

Elements are modelled with
mean values
of the appropriate modulus of elasticity.

Elements are modelled with
final mean values
of the appropriate modulus of elasticity.

At the same time, the effects of actions are stored for both:

• Each load group (set of independent actions: self-weight, variable actions, accidental actions).
• Each design situation (combination of actions).

Combining actions or effects of actions

If Combine Actions is enabled, the effects of actions for each design situation are obtained by first combining forces on members and then computing their overall effect, otherwise the effects are calculated for each load group first and then they are combined to give the design situation value.

In the first case the actions are combined, in the second their effects.

Choice of deformability parameters

Using the mean or using the final mean values of the modulus of elasticity, shear modulus and slip modulus.

The Same Creep Behaviour option discriminates between the use of the effects calculated with the mean values or the final mean values of the elastic material properties.

At ULS the effects of actions are multiplied by partial factors to obtain the design value, and verification is undertaken to demonstrate that they are less than or equal to the design resistances.

The effects of actions used for the verification are those calculated with the mean or final mean elastic modulus depending on the value of the Same Creep Behaviour option.

At SLS, for instantaneous conditions, deflection is always evaluated using the mean value of the modulus of elasticity.

At SLS, for final conditions:

• If Same Creep Behaviour is checked (true), the instantaneous deflection is evaluated for each independent load group, using the mean values of the modulus of elasticity, then the overall final deflection is obtained by combining these values using the k_def  deformation factor:
  ufin,G = uinst,G (1 + kdef)
and
ufin,Q,1 = uinst,Q,1 (1 + ψ2 kdef)
and
ufin,Q,i = uinst,Q,i (ψ0 + ψ2 kdef)
• If Same Creep Behaviour is not checked (false), the final deflection is evaluated by superimposing the deflection obtained for the quasi-permanent combination of actions with the final mean values of the modulus of elasticity, on the difference between the deflections obtained with the mean values of the modulus of elasticity for the characteristic load combination less the quasi-permanent combination. If u_qp,fm =  final deflection for the quasi-permanent combination with final mean elastic modulus, u_qp,m = instantaneous deflection for the quasi-permanent combination with mean elastic modulus and u_ch,m = instantaneous deflection for the characteristic combination with mean elastic modulus, then u_fin = u_qp,fm + (u_ch,m – u_qp,m)

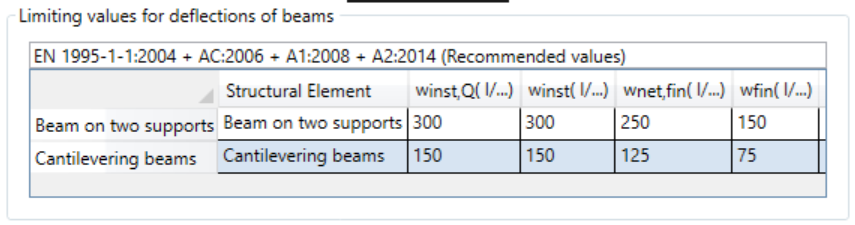
The deflection check of timber beams

In APF WoodBeam and in APF WoodTruss, the verification is carried out for:

• instantaneous deflection  —  due to the total loads (permanent and variable)
• instantaneous deflection  —  due to the variable loads only
• final deflection  —  due to the combination of all actions

The programs normally perform all these verifications, but it is possible to leave only one of them active, or to specify different limits for each one.